详细解释算法的原理以及计算过程。
这是由俄罗斯科学家 Vladimir Levenshtein 在 1965 年提出的这个概念。计算两个文本之间,从第一个文本转换成第二个文本所使用最少的步骤。
对一个文本进行以下三种操作
- 替换一个字符
- 删除一个字符
- 添加一个字符
定义
如果分别用 |a| 和 |b| 表示 a,b 两个字符串的长度,那么它们的列文斯坦距离为 leva,b(|a|,|b|),它符合:
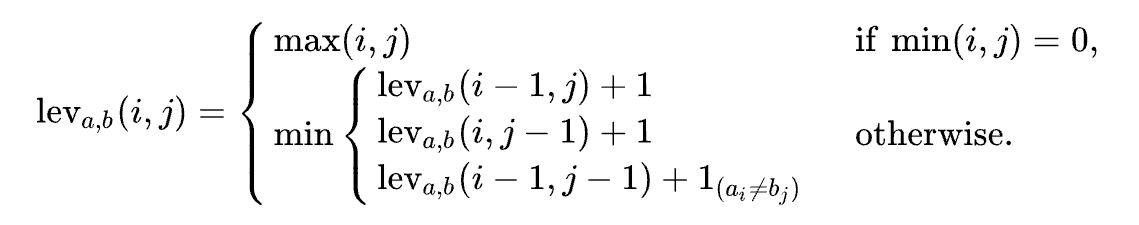
l(ai≠bj) 是一个指示函数,当 ai = bj 时,其值为 0,其他时候它等于 1 。
leva,b(i,j) 表示 a 的前 i 个字符与 b 的前 j 个字符之间的列文斯坦距离。(i 和 j 都是从 1 开始的下标)
注意:min运算中的第一个公式代表( 从 a 中)删除字符(以到达 b);第二个公式代表插入字符;第三个代表替换(取决于当前字符是否相同)。
代码
function levenshteinDistance (a, b) {
const m = a.length
const n = b.length
const d = []
for (let i = 0; i <= n; i++) d[i] = [i]
for (let j = 0; j <= m; j++) d[0][j] = j
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= m; j++) {
d[i][j] = a[j - 1] === b[i - 1] ? d[i - 1][j - 1] : Math.min(d[i - 1][j], d[i][j - 1], d[i - 1][j - 1]) + 1
}
}
return d[n][m]
}
$ lev_ {a,} $ b(|a|,|b|)
原理
例如计算 horse 单词转换成 ros 单词需要使用的最少步骤。
结果是最少需要三个步骤,算法如下:
步骤一:horse > rorse ("h" 替换 "r")
步骤二:rorse > rose (删除 "r")
步骤三:rose > ros (删除 "e")
实例
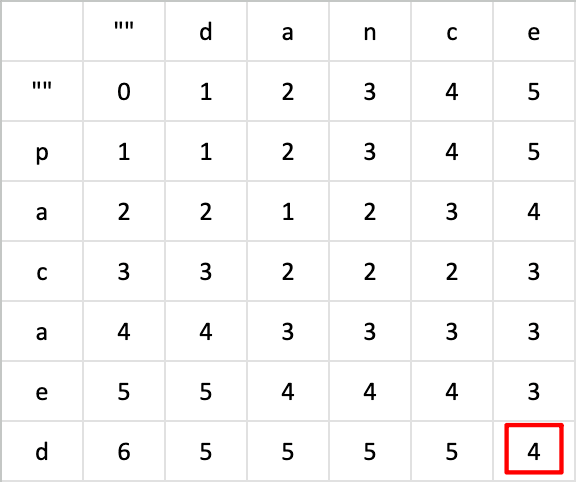
例如,计算 dance 转换成 pacaed 需要使用最少的步骤。(这个词是我作为例子生造的,没有其它特殊意义。)
那么先将这两个单词的每一个字符列出一个矩阵,每个单词的的开头保留一个空值。

先来计算第一行。两个空值是一致的,不需要进行任何的操作,所以将一个空值转换成空值,需要使用最少的步骤是 0。

将一个空值和 d 转换成空值,已知第一个步骤不需要进行任何的操作,但是第二个字符是多余的,需要将 d 删除,所以将空值和 d 转换成空值最少需要用到的步骤是 1。

那么继续往右计算,将一个空值和 da 转换成空值。和空值对比,da 是多余的字符,所以需要两个删除字符的步骤才能转换成和空值一致。
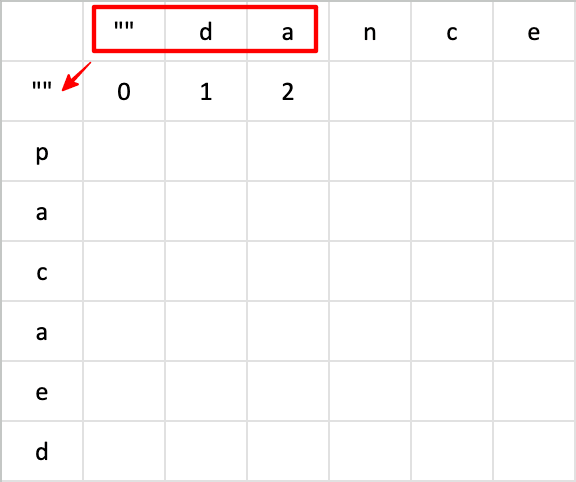
那么后面以此类推都是一样的,这里就可以“偷个懒”,往右直接加 1 就可以了。因为后面比空值都多一个字符,所以都需要多一个删除字符的步骤。

纵列也是一样的算法,将空值转换成空值和 p,需要使用删除字符,将 p 删掉,所以需要用到的步骤是 1。

下面的算法一样,直接往下加 1 即可。
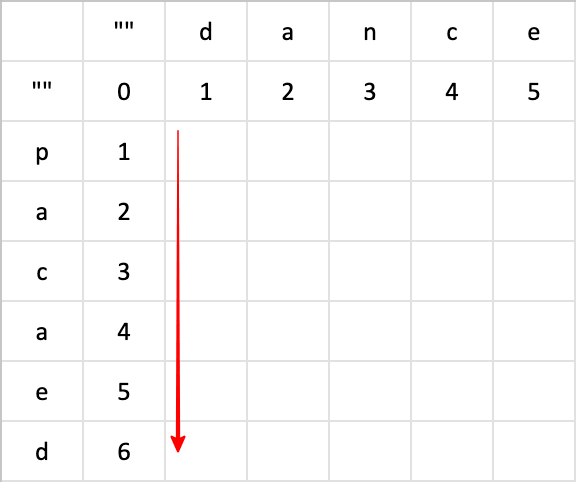
继续计算第二行,将空值 d 转换成空值 p 所需的步骤,只需要将 d 替换成 p,所以需要用到的步骤是 1。计算的原理是这样的,如果遇到很长的字符这样算起来就太慢,下面介绍一个便捷的算法,先对比当前对应的字符是否一致。
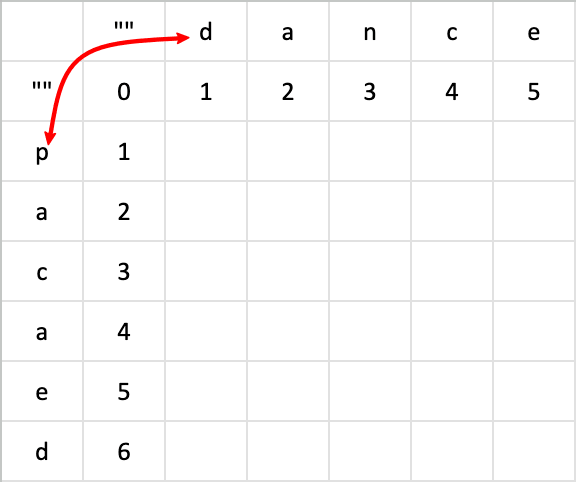
如果不一致,就从矩阵中取这个范围内最小的值,也就是 0,然后再加 1。
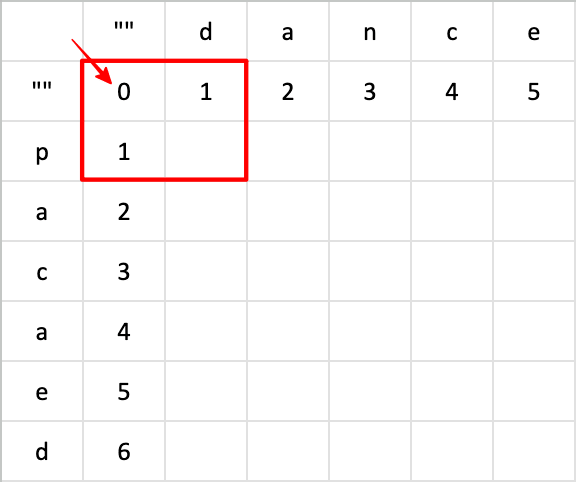
那么就得出了将将空值 d 转换成空值 p 所需的步骤。

后面也是一样的算法,判断 a 和 p 是否一致,如果不一样,从矩阵中取这个范围内最小值,也就是 1,再加上 1。
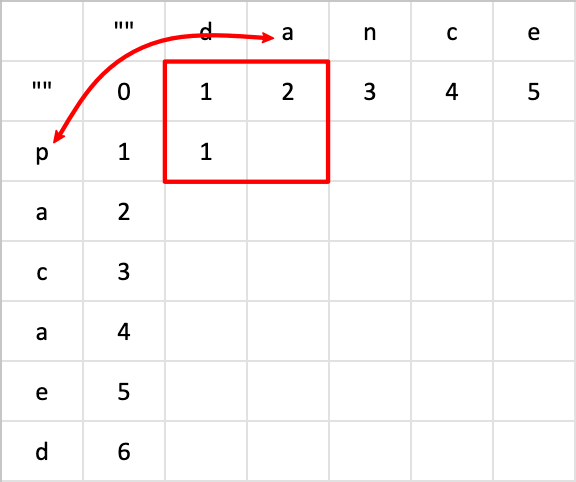
那么就得出了将将空值 da 转换成空值 p 所需的步骤是 2。

还有一个更便捷的计算方法,判断在所有的范围里,是否包含 p,若不包含,根据上面的步骤,先计算出第一个所需的步骤,然后往后加 1 即可。

下面也是一样的算法, 先判断对应的字符,a 和 d 是否一致,若是不一致,从矩阵中取这个范围内最小值再加上 1。

所以得出的结果是 2。

如果对应字符一致,只需要从矩阵中取这个范围最小值,不需要加 1,因为相同的两个字符不需要任何的操作。

所以结果是 1。

后面的内容和 a 都不一致,从矩阵中取这个范围的最小值,也就是 1。因为 n 和 a 是不一致的,需要将最小值再加 1。剩下的往右加 1 即可。

继续往下计算,对应的 c 和 d 不一致,从矩阵中取这个范围内最小值再加上 1。

结果是 3。

往右也是一样的算法,判断 a 和 c 是否一致,如果不一致,从矩阵中取这个范围内最小值再加上 1。

不过需要注意的是最小值的位置不固定,可能会在第二个格子,也有可能会在第一个格子,所以不管存在哪个位置都取最小值。因为我看到有些解释是从第一个格子取值,但是这样的算法并不准确,在某些情况下会算错。
后面的算法都是一样的,就不一一举例了,只需要注意当前要计算对应的字符是否一致,判断是否需要加 1。
全部算完后,右下角的格子就是最终的结果,也就是说从 dance 转换成 pacaed 最少需要四个步骤。